ساختمان داده ها و الگوریتم
الگوریتم :
به مجموعه ای از دستورالعمل ها که هدف خاصی را دنبال می کند الگوریتم می گویند و دارای شرایط زیر است:
1. هر الگوریتم ممکن است هیچ ، یک یا چند ورودی داشته باشد.
2. هر الگوریتم می تواند هیچ ، یک یا چند خروجی داشته باشد .
3. هر الگوریتم بایستی بدون هیچگونه ابهام در دستورالعمل ها بیان شود .
4. الگوریتم باید نهایتاً پایان پذیر باشد .
ساختمان داده ها :
ساختارهایی که جهت دریافت داده های خام به شکل مناسب در کامپیوتر پیاده سازی شده و الگوریتم های مختلف روی آنها اجرا می شود .
تابع بازگشتی :
تابعی است که به طور مستقیم یا غیر مستقیم خود را فراخوانی می کند ، هر تابع بازگشتی دو حالت دارد :
1. حالت بدیهی که در واقع شرط توقف کار است .
2. حالت بازگشتی که در این حالت تابع به شکل مناسب خودش را صدا می زند .
مثال اول :
تابعی بنویسید که به صورت بازگشتی مقدار !n را محاسبه کند .
قسمت آبی رنگ حالت بدیهی و قسمت قرمز رنگ حالت بازگشتی می باشد .
int fact ( int n )
{
if ( n==1 )
return 1;
else
return n * fact ( n-1);
}
5! =120
5*4! =24
4*3! =6
3*2! =3
2*1! =2
1
N! = N * ( N - 1 ) ! .
5! = 1*2*3*4*5 = 120
6! = 1*2*3*4*5*6 = 720
مثال دوم :
تابعی بنویسید که دو عدد a , b را گرفته و به صورت بازگشتی حاصل a به توان b را محاسبه کند .
int pow( int a , int b )
{
if ( b==1 )
return a ;
else
return a*pow( a,b-1);
}
در این مثال a برابر با عدد 2 و b برابر با عدد 3 می باشد .
23=8
23=2*22
2*21
2
مثال سوم :
تابعی بنویسید که عدد n را گرفته و جمله n ام سری فیبوناچی را محاسبه کند .
1 1 2 3 5 8 ..... n
int fibo ( int n )
{
if ( n==1 || n==2 )
return 1 ;
else
return fibo (n-1) + fibo ( n-2 ) ;
}

fibo ( 5 )
fibo ( 4 ) + fibo ( 3 )
fibo ( 3 ) + fibo ( 2 ) fibo ( 2 ) + fibo ( 1 )
fibo ( 2 ) + fibo ( 1 )
مثال چهارم :
تابعی بنویسید که دو عدد a و n را گرفته n امین رقم سمت راست عدد a را برگرداند .
f = (4536271 , 3) = 5
int b ( int a , int n )
{
if ( n == 1 )
return a % 10 ;
else
return b ( a / 10 , n - 1 ) ;
}
4567 % 10 = 7 b = 3
456 % 10 = 6 b = 2
45 % 10 = 5 b = 1
جستجوی دودویی یا binary search
مثال : تابع جستجوی دودویی را به صورت بازگشتی بنویسید.
نکته : در صورتی که آرایه از قبل مرتب شده باشد از این طریق استفاده می کنیم .
در این مثال به دنبال عدد 28 هستیم :
int bin search ( a , x , low , high )
{
if ( low > high )
return -1 ;
mid = ( low + high ) / 2 ;
if ( x == a [ mid ] )
return mid ;
else if ( x > a [ mid ] )
return bin search ( a , x , mid + 1 , high ) ;
else
return bin search ( a , x , low , mid - 1 ) ;
}
| 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 35 | 32 | 28 | 25 | 20 | 19 | 15 | 12 | 10 | 9 | 8 | 7 | 5 |
| high | low | mid | low | mid | low |
تمرین اول (homework):
تابعی بنویسید که دو عدد m و n را گرفته بزرگترین مقسوم علیه مشترک آنها را محاسبه کند .
int bmm( int m , int n )
{
if ( n==0 )
return m ;
else
return bmm ( n , m%n );
}
مثال :
m=80
n=13
80/13=6
6*13=78
80-78=2
حال b را به جای a می بریم و تقسیم بر باقیمانده می کنیم ، تا جایی که باقیمانده برابر با صفر نشده ( یعنی به شرط نرسیده ایم ) ادامه می دهیم.
13/2=6
2*6=12
13-12=1
2/1=2
2*1=2
2-2=0
حال به شرط رسیده ایم و بزرگترین مقسوم علیه مشترک بین اعداد 80 و 13 عدد 1 می باشد
تمرین دوم (homework ) :
تابعی بنویسید که به صورت بازگشتی دو عدد a و b را گرفته و حاصل a*b را محاسبه کند .
int mul ( int a , int b )
{
if ( b==1 )
return a;
else
return a+mul(a,b-1);
}
مثال :
a=6
b=4
a*b=24
6*4=24
6+mul(a,b-1) 24
6+mul(a,3) 18
6+mul(a,2) 12
6+mul(a,1) 6
تمرین سوم ( home work ) :
تابعی بنویسید که به صورت بازگشتی مساله برج های هانوی را حل کند .
حالت اولیه :
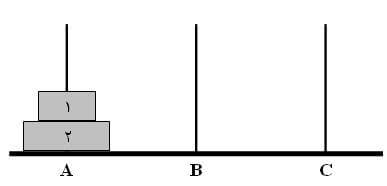
حالت درخواستی :
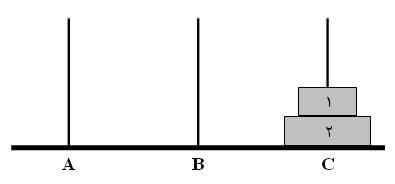
جلسه دوم :
پشته ( stack )
پشته مجموعه ای است مرتب از اقلام داده که درج یک عنصر در آن و حذف از آن از یک طرف انجام می گیرد که به آن بالای پشته می گویند .
نکته : در پشته فقط به عنصر بالای پشته می توان دسترسی داشت . در پشته عنصری که در ابتدا وارد می شود بعد از خروج تمام عناصر خارج می شود ، همچنین عنصری که بعد از بقیه عناصر وارد می شود قبل از همه خارج می گردد ، بنابراین پشته از قانون ( Last in first out ( LIFO تبعیت می کند .
همانطور که میبینید اگر بخواهیم cd آخر را برداریم باید به ترتیب از بالا شروع کنیم و یکی یکی cd ها را برداریم تا به cd آخر برسیم.
اعمال مجاز روی پشته :
1- تست خالی بودن پشته
تابع قابل استفاده برای این عمل تابع (isempty(s می باشد که وظیفه آن در صورتی که پشته s خالی باشد برگرداندن مقدار true است ، در غیر این صورت مقدار false را برمی گرداند .
2- تست پر بودن پشته
تابع قابل استفاده (full(s می باشد که اگر پشته پر باشد مقدار true را برمی گرداند ، در غیر این صورت مقدار false را بر می گرداند .
3- درج عنصر جدید در پشته
تابع قابل استفاده (push(s,x می باشد که عنصر جدید x را در بالای پشته خالی s قرار می دهد .
نکته : تلاش برای درج عنصر در یک پشته پر را overflow یا سر ریز می گویند .
4- حذف عنصر از بالای پشته
تابع قابل استفاده (x=pop(s می باشد که عنصر بالای پشته غیرخالی را حذف کرده و درون متغیر x قرار می دهد .

نکته : تلاش برای حذف عنصر از یک پشته خالی را underflow می گویند .
5- تعیین عنصر بالای پشته
تابع قابل استفاده (x=top(s می باشد که عنصر موجود در بالای پشته غیرخالی s را بدون حذف کردن درون متغیر x می ریزد .
به دلیل طولانی بودن کدهای برنامه در این بخش کدها به صورت شبه کد نوشته شده است .
کاربردهای پشته
1- چاپ برعکس داده های ورودی
s=the empty stack
cin >> s ;
while ( x = ! 0 )
{
push ( s , x ) ;
cin >> x ;
}
while( ! isempty ( s ) )
{
cout << pop ( s ) ;
}
2- چک کردن بالانس بودن پرانتزها
الف ) عبارت را از چپ به راست و symbol به symbol بخوانید و به صورت زیر بررسی کنید :
1. اگر symbol پرانتز باز بود در پشته قرار می گیرد .
2. اگر symbol پرانتز بسته بود عنصر بالای پشته از پشته خارج می شود ، در این حالت اگر پشته خالی باشد یعنی تعداد پرانتزهای بسته بیشتر از پرانتزهای باز یا پرانتز بسته قبل از پرانتز باز است .
ب ) در پایان پیمایش پشته باید خالی باشد ، اگر خالی نباشد خطا رخ داده که در این حالت تعداد پرانتزهای باز بیشتر از تعداد پرانتزهای بسته است .
valid = true ;
stk = the empty stack
while ( ! end of input expression )
{
symb = the next symbol ;
if ( symb == " ( " )
push ( stk , symb ) ;
if ( symb == " ) " )
{
if ( isempty ( stk ) )
valid = false ;
else
x = pop ( stk ) ;
}
}
if ( ! isempty ( stk ) )
valid = false ;
return valid ;
3- مرتب کردن درجی ( insert sort )
با استفاده از دو پشته
s1 , s2 = two empty stacks
cin >> x ;
while ( x != 0 )
{
while ( ! isempty (s1) ) && top (s1)
{
y = pop ( s1 ) ;
push ( s2 , y ) ;
}
push ( s1 , x ) ;
while ( ! isempty ( s2 ) )
{
y = pop ( s2 ) ;
push (s1 , y ) ;
}
cin >> x ;
while ( ! isempty ( s1 ) )
cout << pop ( s1 ) ;
}
home work1:
علاوه بر چک کردن پرانتزها ، کروشه ها و براکت ها را نیز چک کنید .
a = true ;
stk = the empty stack
while ( ! end of input expresson )
{
s = the next symbol ;
if ( s== "(" || s== "[" || s== "{" )
push ( stk , s ) ;
if ( s== ")" || s== "]" || s== "}" )
{
if ( isempty ( stk ) )
a = false ;
else
x = pop ( stk ) ;
}
}
if ( ! isempty ( stk ) )
a = false ;
return a ;
home work2:
شبه کدی بنویسید که متنی را از ورودی خوانده و به صورتهای مختلف زیر چاپ کند :
صورت اول ( با استفاده از یک پشته )
ورودی
This is a test
خروجی
tset a si sihT
در این مثال فرض می کنیم پایان عبارت با علامت * اعلام می شود.
s = isempty stack
cin >> n ;
while ( n != " * " )
{
while ( n != " " )
{
push ( s , n ) ;
cin >> n ;
}
while ( ! isempty ( s ) )
{
cout << pop ( s ) ;
}
cout << " " ;
}
صورت دوم ( با استفاده از دو پشته )
ورودی
This is a test
خروجی
test a is This
در این مثال فرض می کنیم پایان عبارت با علامت * اعلام می شود.
s1 , s2 = two empty stacks
cin >> x ;
while ( x != " * " )
{
push ( s1 , x ) ;
cin >> x ;
}
while ( ! isempty ( s1 ) )
{
m = pop ( s1 ) ;
while ( x != " " || empty ( s1 ) )
{
push ( s2 , m ) ;
m = pop ( s1 ) ;
}
while ( ! isempty ( s2 ) )
{
cout << pop ( s2 ) ;
}
cout<<" ";
}
صورت سوم ( با استفاده از یک پشته )
ورودی
This is a test
خروجی
sihT si a tset
در این مثال فرض می کنیم پایان عبارت با علامت * اعلام می شود.
s = isempty stack
cin >> n ;
while ( n != " * " )
{
while ( n != " " )
{
push ( s , n ) ;
cin >> n ;
}
while ( ! empty ( s ) )
{
cout << pop ( s ) ;
}
cin >> n ;
}
مبحث بعد
نحوه نمایش عبارت ها
1- روش پسوندی (post fix )
در این روش عملگر بعد از عملوند خود می آید . + a b
مثال : a * b + c
a b * c +
2- روش میانوندی ( in fix )
در این روش عملگر بین دو عملوند خود می آید . a + b
a * b + c
3- روش پیشوندی ( prefix )
در این روش عملگر قبل از دو عملوند خود می آید . a b+
مثال : a * b + c
+ * a b c
اولویت عملگرها ( صرفاً جهت اطلاع )
علامت $ به معنی توان است ، اگر در یک عبارت چندین توان داشتیم برعکس بقیه عملگرها که از چپ به راست اولویت بندی می شوند ، توان را از راست به چپ اولویت بندی می کنیم .
هر گاه پرانتزهای تودرتو داشتیم ، ابتدا پرانتز داخلی بعد به ترتیب از چپ به راست محتوای پرانتز ها را اولویت بندی می کنیم ، دقت داشته باشید که خود پرانتز اولویت بندی نمی شود بلکه محتوای آن مد نظر است .
( )
$
* /
+ -
مثال 1 :
in fix : a * b + c
حالت میانوندی را به دست آورده ایم ، حال حالت prefix و post fix را به دست می آوریم .
prefix : + * a b c
post fix : a b * c +
مثال 2 :
in fix = a + b * c $ d / e - g * h
prefix = - + a / * b $ c d e * g h
post fix = a b c d $ * e / + g h * -
home work1 (جلسه سوم )
حالت های prefix و post fix را به دست آورید.
in fix : a + ( b / ( c - d ) ) $ e * f / ( g + h )
prefix : + a / * $ / b / c d e f + g h
post fix : a b c d - / e $ f * g h + / +
جلسه سوم
کاربردهای stack
ارزیابی عبارت post fix
نکته : عبارت oprand ورودی می گیرد و تشخیص می دهد عملگر است یا عملوند ، اگر عملوند باشد true را بر می گرداند و اگر عملگر باشد false را بر می گرداند .
نکته : عبارت eval دو عملوند و یک عملگر را می گیرد و عملگر را روی عملوندها محاسبه می کند .
s = the empty stack
while ( ! end of post fix expression )
{
opr = the next symbol
if ( is oprand ( opr ) )
push ( s , opr ) ;
else
{
op1 = pop ( s ) ;
op2 = pop ( s ) ;
value = eval ( op1 , opr , op2 ) ;
push ( s , value ) ;
}
}

 اطلاعات مورد نیاز دانشجویان رشته نرم افزار کامپیوتر
اطلاعات مورد نیاز دانشجویان رشته نرم افزار کامپیوتر