ساختمان داده ها و الگوریتم
تبدیل عبارت infix به post fix
فرض کنید عملگر op1 در عبارت infix قبل از عملگر op2 ظاهر شده باشد:
در این صورت تابع :
prcd ( op1 , op2 )
در صورتی که اولویت عملگر op1 از اولویت عملگر op2 بیشتر باشد مقدار true را بر می گرداند و در غیر این صورت مقدار false را بر می گرداند .
مثال
a + b - c : prcd ( + , - ) True
a + b * c : prcd ( + , * ) False
a / b / c : prcd ( / , / ) True
a $ b $ c : prcd ( $ , $ ) False
تبدیل infix به post fix :
infix = a + b * c $ d
post fix = a b c d $ * +
برای این کار عبارت از سمت چپ به راست ارزیابی می شود اگر symbol مورد نظر عملوند بود آن را در خروجی چاپ می کنیم و به سراغ symbol بعدی می رویم ، اگر symbol عملگر بود تا زمانی که پشته خالی نشده یا نتیجه تابع :
prcd ( top , عملگر جاری )
true باشد از پشته pop می کنیم و در خروجی چاپ می کنیم ، بعد از این مرحله در صورت false شدن prcd عملگر را درون stack قرار می دهیم ، زمانیکه به پایان عبارت رسیدیم کل محتویات پشته را pop کرده و چاپ می کنیم .
s = the empty stack
while ( ! end of infix expression )
{
rd = next symbol ;
if ( is operand ( rd) )
cout<< rd ;
else
{
while ( ! empty (s) && prcd ( top (s) , rd ) == true )
cout << pop ( s ) ;
push ( s , rd ) ;
}
}
while ( !empty (s) )
cout << pop ( s ) ;
homework 1
برنامه فوق را به گونه ای تغییر دهید که عبارتهای شامل پرانتز را از infix به post fix تبدیل کند .
تبدیل infix به prefix :
برای این الگوریتم کافی است از الگوریتم تبدیل infix به post fix استفاده کنیم ، با این تفاوت که بایستی عبارت را از آخر به اول ارزیابی کنیم و هر جا ")" بود "(" در نظر بگیریم ، و هر جا "(" بود ")" در نظر بگیریم ، در نهایت عبارت به دست آمده را برعکس کرده و چاپ می کنیم .
homework 2
شبه کد الگوریتم بالا را بنویسید .
پیاده سازی پشته توسط آرایه
آرایه item :
| max s-1 | ......... | 2 | 1 | 0 | نام خانه آرایه |
| ......... | 3 | 2 | 1 | مقدار |
پشته s :
| 3 |
| 2 |
| 1 |
در این مثال
نام آرایه : item
نام پشته : s
منظور از max s مقدار ظرفیت پشته s می باشد .
push
push ( s , x )
{
if ( ! full ( s ) )
{
s . top ++ ;
s . item [ s . top ] = x
}
}
با این برنامه می توان n عدد را گرفته و برعکس چاپ کرد .
{
private :
int maxsize ;
int top ;
int * item s ;
void stack full ( ) { cout << " stack overflow " ; exit ( 1 ) ; }
void stack empty ( ) { cout << " stack underflow " ; exit ( 1 ) ; }
public
sstack ( int max stack =100 ) ;
~ sstack ( ) ;
bool empty ( ) { return ( top == -1 ) ; }
bool full ( ) { return ( top == maxsize -1 ) ; }
void push ( int ) ;
int pop ( ) ;
int stack top ( ) ;
} ;
sstack : : sstack ( int ms )
{
maxsize = ms ;
item = new int [ ms ] ;
top = -1 ;
}
~ sstack : : sstack ( )
{
delete [ ] item ;
}
void sstack : : push ( int x)
{
if ( full ( ) )
stack full ( ) ;
else
{
top ++ ;
item s [ top ] = x ;
}
}
int sstack : : pop ( )
{
if ( empty ( ) )
stack empty ( ) ;
else
{
int x ;
x = item s [ top ] ;
top -- ;
return x ;
}
}
int sstack : : top ( )
{
if ( empty ( ) )
stack empty ( ) ;
else
next item s [ top ] ;
}
main ( )
{
int n , x ;
cin >> n ;
sstack s ( n ) ;
for ( int i=0 ; i < n ; i ++ )
cin >> x ;
s . push ( x ) ;
}
while ( ! s . empty ( ) )
{
x = s . pop ( ) ;
cout << x ;
}
جلسه پنجم
* در کل مثال های این جلسه نام آرایه items می باشد .
صف ( queue )
ساختار queue به صورت FIFO به معنی First in First out می باشد .

توابع بخش queue :
چند نمونه از کاربردهای صف :
1- صف تشکیل شده از اطلاعات ارسالی هنگام چاپ کردن اطلاعات .
2- صف موجود در صفحه کلید .
3- شبیه سازی صف های معمولی .
مثال : شبه کدی که بزرگترین عنصر موجود در یک صف را به انتهای صف ببرد :
{
if ( empty ( q1 ) )
return ;
else
}
max = remove ( q1 ) ;
insert ( q2 , max ) ;
while ( ! empty ( q1 ) )
{
x = remove ( q1 ) ;
if ( x > max )
max = x ;
insert ( q2 , x ) ;
}
c = 0 ;
while ( ! empty ( q2 ) )
{
x = remove ( q2 ) ;
if ( max == x )
c + + ;
else
insert ( q1 , x ) ;
}
for ( i = 0 ; i < c ; i + + )
insert ( q1 , max ) ;
}
پیاده سازی queue :
1- توسط آرایه :
الف ) حرکت اندیس های rear و front
rear ( درج کردن ) : اول به جلو می رود بعد وارد می کند .
front ( حذف کردن ) : اول حذف می کند بعد به جلو می رود .
مشکل این روش اتلاف حافظه زیاد است .
{
if ( ! full ( q ) )
{
q = rear + + ;
q . items [ q . rear ] = x ;
}
}
{
if ( q . rear == max q - 1 )
return true ;
else
return false ;
}
{
if ( ! empty ( ) )
{
x = q . items [ q . front ] ;
q . front + + ;
}
}
{
if ( q . rear < q . front )
return true ;
else
return false ;
}
{
x = q . items [ 0 ] ;
for ( i = 0 ; i < q . items ; i + + )
q . items [ i ] = q . items [ i + 1 ] ;
q . rear - - ;
}
توابع این بخش عبارت اند از :
{
if ( q . rear == q . front )
return true ;
else
return false ;
}
{
if ( ! empty ( q ) )
{
if ( q . front == max - 1 )
q . front = 0 ;
else
q . front + + ;
x = q . items [ q . front ] ;
}
}
{
if ( ! full ( q ) )
{
if ( q . rear == max - 1 )
q . rear = 0 ;
else
q . rear + + ;
q . items [ q . rear ] = x ;
}
}
{
k = q . rear ;
if ( k == max - 1 )
k = 0 ;
else
k + + ;
if ( k = q . front )
return true ;
else
return false ;
}
صف اولویت ( pq ) :
صفی است که در آن بین عناصر موجود در صف ، اولویت خاصی برقرار است .
انواع صف اولویت :
1- صف اولویت صعودی :
2- صف اولویت نزولی :
اعمال مجاز روی صف اولویت :
تست خالی بودن صف :
این تابع مقدار true را بر می گرداند اگر صف اولویت pq خالی باشد ، در غیر این صورت مقدار false را بر می گرداند .
تست پر بودن صف :
این تابع مقدار true را بر می گرداند اگر صف اولویت pq پر باشد ، در غیر این صورت مقدار false را بر می گرداند .
درج عنصر جدید در صف اولویت :
حذف عنصر از صف اولویت :
مثال : شبه کدی که بیست عدد را از ورودی خوانده ، آنها را به صورت نزولی چاپ کند :
dpq = the empty desending precendence queue
for ( i = 0 ; i < 20 ; i + + )
{
cin >> x ;
}
while ( ! empty ( dpq ) )
{
x = pq maxdelete ( dpq ) ;
cout << x ;
}
homework2 : یکی از عملیاتهای بالا را انجام دهید .
در روش اول عناصر موجود در صف بایستی جابه جا شوند تا به صورت مرتب شده در آیند که این کار بسیار وقت گیر است .
در روش دوم بعد از حذف عنصر از صف بقیه عناصر باید جابه جا شوند که این موضوع نیز بسیار وقت گیر است ، این وقت گیر بودن در صورتی است که از آرایه برای نگهداری عناصر صف اولویت استفاده شود ، پس پیاده سازی صف اولویت با آرایه مقرون به صرفه نیست .
جلسه ششم
لیست پیوندی ( Linked List ) :
تعاریف :
لیست خالی
لیستی است که اشاره گر خارجی آن null می باشد .
نکته : لیست پیوندی ساختمان داده ای پویا است به این معنا که تعداد گره های آن در حین اجرای برنامه تغییر می کند .

توابع لیست پیوندی :
مثال 1
مثال 2
نکته : در شمارش سرلیست حساب نمی شود .
%99 از مواقع می توان با حلقه for لیست پیوندی را انجام داد .
مثال 3
اگر در انتهای حلقه for علامت " ; " بود ، حلقه فقط به دور خودش می چرخد و دستوری را اجرا نمی کند .
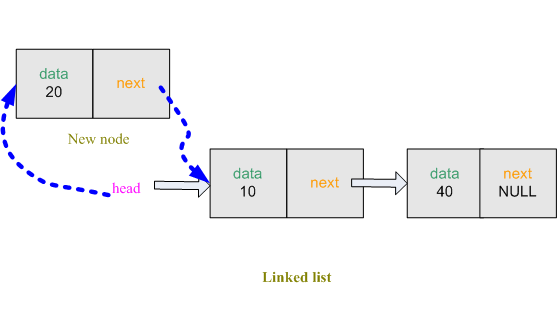
پیاده سازی پشته به وسیله لیست پیوندی
مثال 4
تابعی به نام instail که گره ای با محتوای x را در انتهای لیست L قرار دهد .
مثال 5
پیاده سازی صف با استفاده از لیست پیوندی
مثال 6
تابعی به نام insafter که گره ای با محتوای x را بعد از گره p درج کند .
ادامه مثال های جلسه قبل
مثال 7 : تابعی که گره بعد از گره p را حذف کند .
مثال 9 : تابعی که کلیه گره های موجود بین گره های p و q را حذف کند و محتویات آنها را درون آرایه a قرار دهد.
home work 1 : تابعی بنویسید که گره ای با محتوای x را طوری در لیست مرتب L درج کند تا لیست همچنان مرتب باقی بماند ( لیست به صورت صعودی مرتب است ) .
{
q = null ;
p = L;
while ( p ! = null && x > info ( p ) )
{
q = p ;
p = next ( p ) ;
}
if ( q == null )
inshead ( L , x );
else
insafter ( q , x );
}
لیست پیوندی دایره ای
لیستی است که آدرس اولین گره در گره آخر می باشد ، در این حالت هر گره می تواند گره اول باشد .
homework 2 : پیاده سازی صف توسط لیست پیوندی دایره ای را انجام دهید .
لیست دو پیوندی
لیست دو پیوندی دایره ای
کاربردهای لیست پیوندی
1 . مسأله نمایش اعداد بزرگ
مثال : حاصل جمع دو عدد زیر
کاربرد دوم لیست پیوندی : چند جمله ایها
{
s = 0 ;
i = 0 ;
p = fx ;
while ( p != null )
{
s = s + ( info ( p ) * pow ( x , i ) ) ;
i ++ ;
p = next ( p );
}
return s ;
}
درخت دودویی
در درخت دودویی هر پدر حداکثر دو پسر دارد .
درخت دودویی محض
اگر در یک درخت دودویی هر گره پدر دقیقاً دو پسر داشته باشد به آن درخت دودویی محض می گویند .
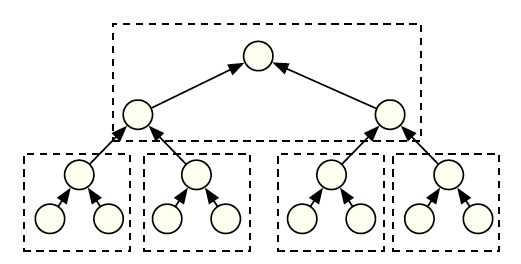
سطح گره های درخت دودویی : Level
ریشه اصلی یا root دارای سطح 0 است و سطح هر گره غیر ریشه یک واحد بیشتر از سطح گره پدرش است .
مثال : اگر یک درخت دودویی در سطح L دارای m گره باشد در سطح L+1 حداکثر چند گره دارد ؟ 2m
مثال : یک درخت دودویی در سطح L حداکثر می تواند چند گره داشته باشد ؟ 2L=L ، 33=9
عمق ( depth ) :
عمق یک درخت دودویی بیشترین سطح برگ های درخت می باشد .
نکته : در یک درخت دودویی محض تعداد کل گره برابر است با :
نمایش درخت دودویی :
برای نمایش درخت های دودویی از لیست پیوندی استفاده می شود .
تعاریف :
ادامه مباحث جلسه قبل :
مثال 1 : تابعی که یک درخت را گرفته و تعداد node های آن را محاسبه کند .
{
if ( tree == null )
return 0 ;
else
return 1 + tree node count ( left ( tree ) ) + tree node count ( right ( tree ) ) ;
}
{
if ( tree == null )
return 0 ;
else
{
if ( left ( tree ) == null && right ( tree ) == null )
return 1 ;
else
return tree leaf count ( leaf ( tree ) ) + tree leaf count ( right ( tree ) ) ;
}
}
{
if ( tree == null )
return 0 ;
else
return 1 + Max ( tree depth ( left ( tree ) ) , tree depth ( right ( tree ) ) ) ;
}
p = get node ( ) ;
info ( p ) = x ;
left ( p ) = right ( p ) = null ;
return p ;
}
{
q = maketree ( x ) ;
left ( p ) = q ;
}
q = maketree ( x ) ;
right ( p ) = q ;
}
مثال 4 : تابعی که درخت را بگیرد و آن را برعکس کند .
{
if ( t1 == null )
t2 = null ;
else
{
t2 = maketree ( info ( t1 ) ) ,
left ( t2 ) = makemirror ( right ( t1 ) ) ,
right ( t2 ) = makemirror ( left ( t1 ) ) ;
return t2 ;
}
}
( ترجیحاً با استفاده از درخت )
جلسه دهم
درخت جستوجوی دودویی( binary search tree ( BST
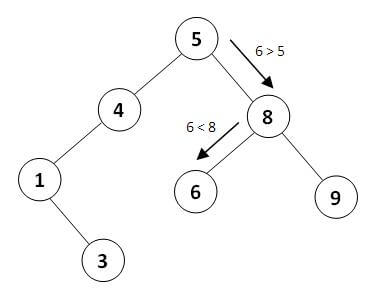
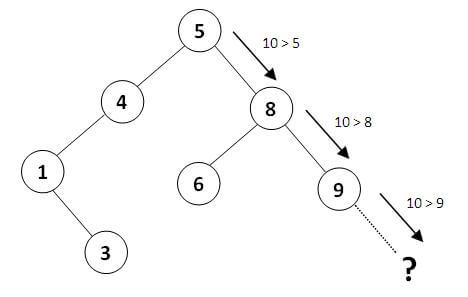
{
if ( x < info ( tree ) )
{
if ( left ( tree ) ! = null )
insBST ( left ( tree ) , x ) ;
else
set left ( tree , x ) ;
}
if ( x > info ( tree ) )
{
if ( right ( tree ) ! = null )
insBST ( right ( tree ) , x ) ;
else
set right ( tree , x ) ;
}
}
شامل عملگرهای دوتایی توسط درخت دودویی
پیمایش درخت های دودویی :
ب ) هر گره دقیقا یک بار ملاقات شود .
روش های پیمایش درخت های دودویی :

1 - روش preorder
الف ) گره ریشه یا پدر را ملاقات کن .
ب ) زیردرخت چپ را به روش preorder ملاقات کن .
2 - روش inorder
الف) زیردرخت چپ را به روش inorder ملاقات کن .
3 - روش postorder
الف) زیردرخت چپ را به روش postorder ملاقات کن .
ب ) زیردرخت راست را به روشpostorder ملاقات کن .
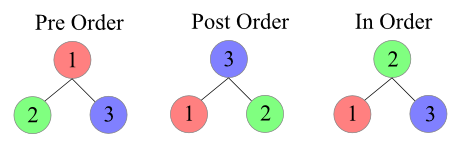
پیاده سازی روش preorder
{
if ( tree == null )
return ;
else
{
cout << info ( tree ) ;
preorder ( left ( tree ) ) ;
preorder ( right ( tree ) ) ;
return ;
}
}
{
if ( tree == null )
return ;
else
{
inordr ( left ( tree ) ) ;
cout << info ( tree ) ;
inorder ( right ( tree ) ) ;
return ;
}
}
{
if ( tree == null )
return ;
else
{
postorder ( left ( tree ) ) ;
postorder ( right ( tree ) ) ;
cout << info ( tree ) ;
return ;
}
}
الگوریتم هافمن
-2 دو کاراکتر با کمترین میزان تکرار
(چگالی) را انتخاب میکنیم.
-3 کاراکتر های مرحله 2 را با کاراکتر جدیدی که دارای چگالی برابر با مجموع چگالی دو کاراکتر فوق است جایگزین
میکنیم.
-4 تا زمانی که فقط یک کاراکتر باقی مانده
باشد، به مرحله 2 میرویم.
-5 از عملیات فوق یک درخت
حاصل می شود، بر روی این درخت هر مسیر به سمت چپ با 0 و هر مسیر به سمت
راست با 1 وزن دهی میشود.
-6 کد
هر کاراکتر با کنار هم گذاشتن وزن ها از ریشه تا آن کاراکتر به دست می آید.



E: 00
M: 0100
W: 0101
C: 0110
H: 01110
U: 01111
N: 100
I: 1010
T: 1011
_: 110
S: 111
همانطور که مشاهده می کنید به حرف E که تعداد تکرار بیشتری داشته کد کوچکتر 00 اختصاص داده شده ، و از این پس در این کد نوشته ای که به روش هافمن فشرده سازی شده حرف E با کد 00 شناخته می شود نه با کد اسکی آن .
جلسه یازدهم
مقدمه ای بر کارایی الگوریتم :
برای حل یک مسأله ممکن است الگوریتم های مختلفی وجود داشته باشد که هر کدام دارای مزایا و معایب خاص خودشان هستند ، کارایی الگوریتم بر اساس دو معیار اندازه گیری می شود ، یکی از آنها بهره وری از فضا و دیگری کارایی زمان است ، در الگوریتم ها آنچه بسیار اهمیت دارد زمان اجرا است ، این زمان تحت تأثیر عوامل متعددی قرار دارد ، یکی از اصلی ترین عوامل تأثیرگذار در زمان پردازش الگوریتم ها اندازه ورودی است ، به عنوان مثال زمان لازم برای مرتب سازی عناصر یک آرایه به تعداد عناصر موجود در آن بستگی دارد بنابراین اگر زمان اجرای الگوریتم را T در نظر بگیریم ، کارایی آن الگوریتم به صورت تابع ( T ( n بیان می شود که n همان اندازه ورودی است ، نوع دستورالعمل ها و سرعت اجرای ماشین نیز در زمان اجرا مؤثر است .
این عوامل به کامپیوتری که مورد استفاده قرار می گیرد بستگی دارد ، نمی توان مقدار ( T ( n را بر اساس واحد های زمان مثل ثانیه بیان کنیم . لذا ( T ( n تعداد تقریبی از دستورالعمل هایی است که باید اجرا شوند ، ( T ( n را پیچیدگی زمانی الگوریتم گویند .
مثال : محاسبه پیچیدگی زمانی و مرتبه الگوریتم مرتب سازی انتخابی :
void select ( int x [ ] , const int n )
{
int min , item ;
for ( int i = 0 ; i < n - 1 ; i ++ )
{
min = i ;
for ( int j = i + 1 ; j < n ; j ++ )
{
if ( x [ j ] < x [ min ] )
min = j ;
}
item = x [ i ] ;
x [ i ] = x [ min ] ;
x [ min ] = item ;
}
}
در این صورت تعداد عناصر آرایه برابر است با :
1 - روش سطری :
 اطلاعات مورد نیاز دانشجویان رشته نرم افزار کامپیوتر
اطلاعات مورد نیاز دانشجویان رشته نرم افزار کامپیوتر